APS105预习 - 01

前言

闲来无事，还是决定重新拾起C，开个新坑充当笔记本+碎碎念。至于rust，要不明天开始？

使用教材

多大教授所写APS105 Computer Fundamentals的电子书

Snefru: Learning Programming with C

也附上Github仓库地址：Github Repository

Chapter 1： Basic structure of computers and Binary systems

计算机中的数据存储方式

在学习C语言之前，对计算机存储数据原理的了解是非常重要的。在现代计算机中，一般使用二进制来存储数据

举个例子：

十进制	二进制
0	00
1	01
2	10
3	11

两位数二进制数字可以存储0-3，以此类推三位数便可存储0-7。

不难发现，n位数字可以表示 $0 \sim (2^n - 1)$ ，同理要表示n个数字，我们需要 $ \log_2(x) $

在现代计算机中，一个字节（byte）由 8 位（bit）组成。千字节（KB）等于 1024 字节。兆字节（MB）等于 1024 千字节。吉字节（GB）等于 1024 兆字节。太字节（TB）等于 1024 吉字节。

数据寻址

所有数据都需要地址，数据两部分，现代计算机使用64-bits来表示地址，一共可以表示 $ 2^64 $个不同的地址，每个地址对应一个字节的数据。也就是说64-bits寻址可以存储16 Exabyte的数据

进制转换

这一部分偏数学，且较容易理解，故放两张图

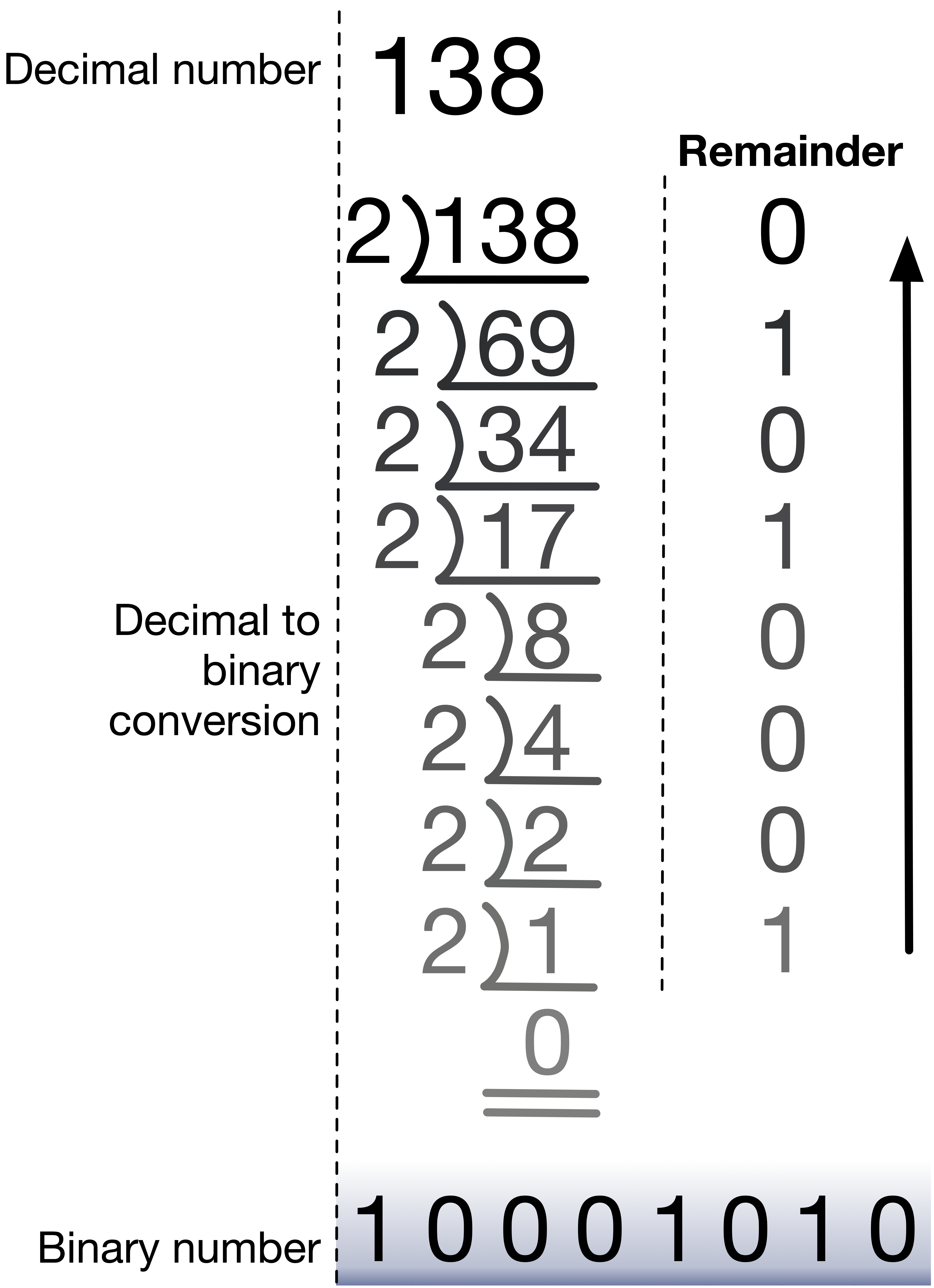
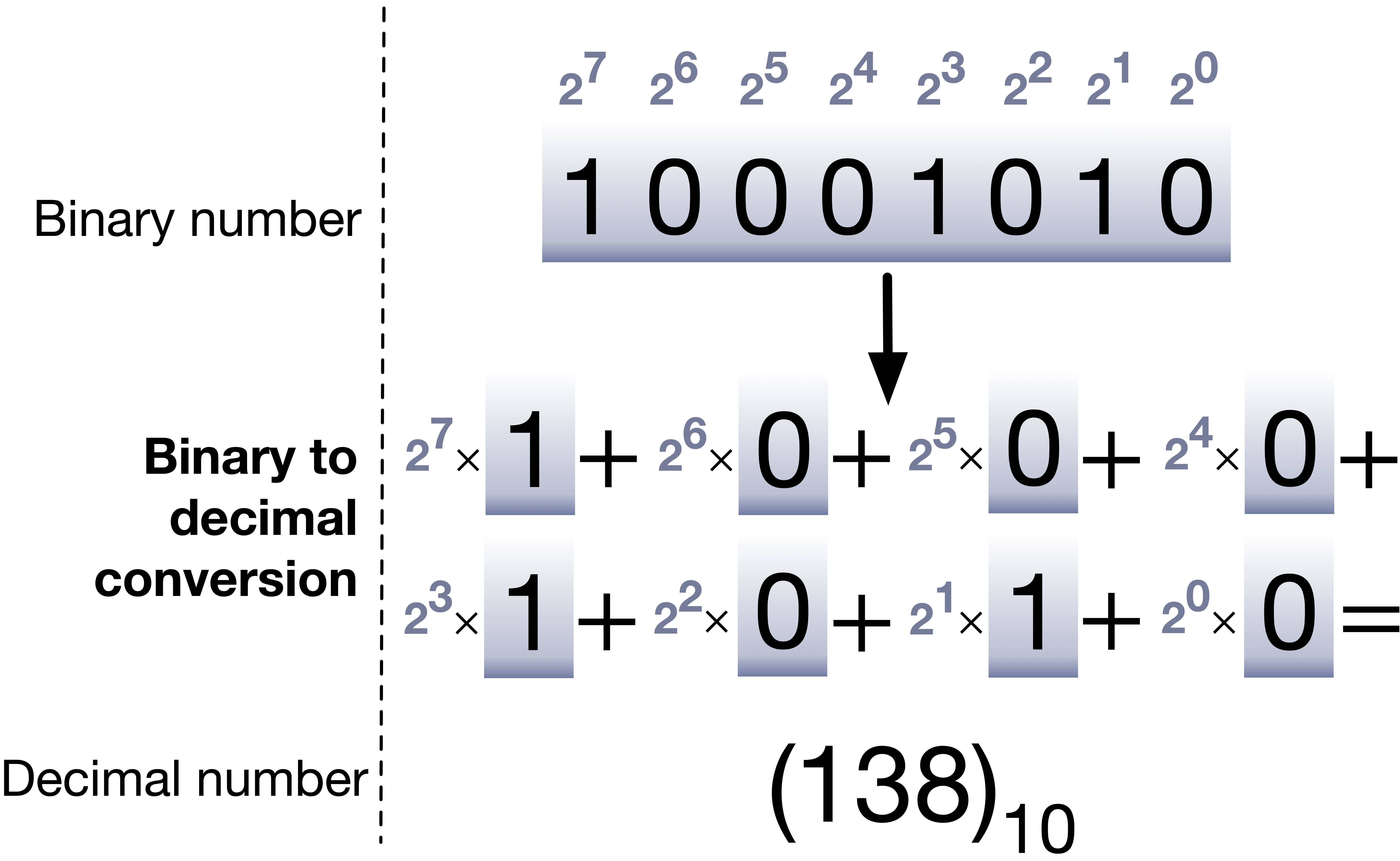
Chapter 2 Data operation and representation

2.2 数据类型与表示

基础数据类型

类型	Format Specifier	说明
int	%d	整数，正或负，4-bytes (32bit)
unsigned int		无符号整数，4-bytes, $ 0 \sim 2^31 - 1$
float	%f	单精度浮点数，4-bytes
double	%lf	双精度浮点数, 8-bytes
char	%c	字符, 1-bytes, 使用ASCII码存储
bool	%d	布尔值, 1-bytes

Boolean

不同于C++， 在C中使用boolean需要导入库：

#include <stdbool.h>

变量初始化

不同与Python等语言，在C/C++中变量在使用前需要显式的声明

如果一个变量没有赋初始值，变量的初始值不是0！相反，初始值会是内存中该位置的值（可以理解为随机值）

使用scanf读取值

#include <stdio.h>

int main(void) {
  int integer = 0;
  float fdecimal = 0.0;
  double ddecimal = 0.0;
  char c;
  printf("Type in: ");
  scanf("%d %f %lf %c", &integer, &fdecimal, &ddecimal, &c);
  printf("Your input is %d %f %lf %c", integer, fdecimal, ddecimal, c);
}

注意，scanf传入的是变量的地址而非变量 （e.g. &integer, &是地址运算符）

2.3 Operations

运算结果是什么类型？

在C中算数运算的结果始终是精度更高的被运算数的类型, 更高精度的数据类型有传染性

举个例子：

int x = 10*5/3; 

上述代码的运算结果会是int 类型，运算结果的小数部分会被无情截断

终极玄学之 ++i与i++

• ++i 是前缀，即递增发生在语句中。因此， j = ++i; 等价于 j = i = i + 1; 。由于赋值运算符的存在，计算是从右到左进行的。

• 而 i++ 是后缀，即对 i 的递增发生在语句之后。这意味着 j = i++; 等价于 j = i; i = i + 1; 。

可以尝试

#include <stdio.h>
int main(void) {
  int i = 1, j = 31;
  j = ++i;  // Equivalent to j = i = i + 1;
  printf("With prefix: i = %d, j = %d\n", i, j);
  i = 1, j = 31;
  j = i++; //Equivalent to j = i; i = i + 1;
  printf("With postfix: i = %d, j = %d\n", i, j);
  return 0;
}

//With prefix: i = 2, j = 2
//With postfix: i = 2, j = 1

类型转换 Type casting

double x = (double) 3/2

sizeof()运算符

用于获取在当前操作系统中用于存储某个数据类型所需的字节数(amount of byte)

2.4 数学库 Math Library

数学符号表示法	函数原型	它有什么作用？	示例
$x$	double sqrt(double x);	返回 x 的平方根	sqrt(4) 返回 2.0
$x^y$	double pow(double x, double y);	返回 x 的 y 次方	pow(2, 3) 返回 8.0
$e^x$	double exp(double x);	返回 e （欧拉数）的 x 次方	exp(1) 返回 2.718281828459045
$\log⁡(x)$	double log10(double x);	返回 x 的以 10 为底的对数	log10(100) 返回 2.0
$\ln⁡(x)$	double log(double x);	返回 x 的自然对数	log(M_E) 2 返回 1.0
$\left |x \right|$	double fabs(double x);	返回 x 的绝对值	fabs(-2) 返回 2.0
$\sin⁡(x)$	double sin(double x);	返回 x 的正弦值，其中 x 以弧度（而非角度）为单位	sin(M_PI * 2) 3 返回 0.0
$\cos⁡(x)$	double cos(double x);	返回 x 的余弦值，其中 x 以弧度（而非角度）为单位	cos(M_PI * 2) 3 返回 1.0
$\tan⁡(x)$	double tan(double x);	返回 x 的正切值，其中 x 以弧度（而非角度）为单位	tan(M_PI) 3 返回 0.0
$\sin^−1⁡(x)$ 或 $\arcsin⁡(x)$	double asin(double x);	返回 x 的反正弦值（以弧度为单位，而非角度）	asin(0.5) 返回 0.523599
$\cos^−1⁡(x)$ 或 $\arccos⁡(x)$	double acos(double x);	返回 x 的反余弦值（以弧度为单位，而非角度）	acos(0.5) 返回 1.047198
$\tan^−1⁡(x)$ 或 $\arctan⁡(x)$	double atan(double x);	返回以弧度（而非角度）表示的 x 的反正切值	atan(2) 返回 1.107149
max(x)	double fmax(double x, double y);	返回 x 和 y 中的最大值	fmax(3.2, -7.9) 返回 3.2
min(x)	double fmin(double x, double y);	返回 x 和 y 中的最小值	fmin(-6.1, -7.3) 返回 -7.3
⌊x⌋	double floor(double x);	返回小于或等于 x 的最大整数，即对 x 向下取整	floor(9.6) 返回 9.0
⌈x⌉	double ceil(double x);	返回大于或等于 x 的最小整数，即对 x 向上取整	ceil(3.09) 返回 4.0
x % y	double fmod(double x, double y);	返回 x / y 的余数 4。请记住， % 运算符仅适用于 int 操作数，而 fmod 也适用于 double 操作数。	fmod(5.3, 2.1) 返回 1.1
⌊x⌉	double rint(double x);	返回最接近 x 的整数，即对 x 进行四舍五入	rint(-2.1) 返回 -2.0